Torsten Warncke - SZ Neustadt Bremen - Mathematik - Analysis mit e-Funktion
1 Vermischte Aufgaben, Lambacher/Schweizer, S. 213
LS führen auf S. 204 die wesentlichen Punkte einer Kurvendiskussion auf: Symmetrie,
Nullstellen und Funktionswert an der Stelle Null, Extrema, Wendepunkte und Graph der
Funktion. Für Extrema und Wendepunkte bestimmen wir zunächst die ersten drei Ableitungen,
wobei nun auch Ketten- und Produktregel Anwendung finden.
1.1 7.a)
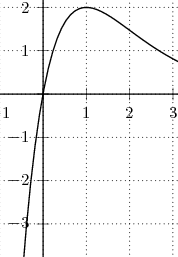
Symmetrie: Weder YAS noch 0PS, da mit
-Funktion.
Ableitungen:
Mittels Produktregel und Kettenregel finden wir:
,
,
,
,
,
,
, also
,
. Analog erhalten
wir und
, alles mit Produktregel und
Ausklammern der e-Funktion.
Schnittpunkte mit den Koordinatenachsen:
Der Schnittpunkt mit der y-Achse ergibt sich über den Funktionswert an der Stelle Null:
.
Schnittpunkte mit der x-Achse ergeben sich über Nullstellen der Funktion :
ist
einzige Nullstelle der Funktion (e-Funktion wird nie Null, EPiNweFNi).
Extrema:
Notwendige Bedingung für Extrema ist
,
d.h. .
EPiNweFNi: -2 und e-Funktion sind nie Null,
wird Null, für .
Einsetzen in
ergibt ,
d.h. es liegt ein Hochpunkt bei
vor. Wir setzen
noch in
ein, um den y-Wert des Hochpunktes zu bestimmen:
,
d.h. .
Wendepunkte:
Notwendige Bedingung für Wendepunkte ist
,
d.h. .
EPiNweFNi: 2 und e-Funktion sind nie Null,
wird Null, für .
Einsetzen in
ergibt ,
d.h. es liegt ein Wendepunkt bei
vor. Wir setzen
noch in
ein, um den y-Wert des Wendepunktes zu bestimmen:
,
d.h. .
1.2 7.c)
Ableitungen:
Mittels Produktregel und Kettenregel finden wir:
,
und
wobei wir wieder die
e-Funktion ausklammern.
Schnittpunkte mit den Koordinatenachsen:
Der Schnittpunkt mit der y-Achse ergibt sich über den Funktionswert an der Stelle Null:
.
Schnittpunkte mit der x-Achse ergeben sich über Nullstellen der Funktion :
ist
einzige Nullstelle der Funktion (e-Funktion wird nie Null, EPiNweFNi).
Extrema:
Notwendige Bedingung für Extrema ist
,
d.h. .
EPiNweFNi: e-Funktion wird nie Null,
.
Einsetzen in
ergibt ,
d.h. es liegt ein Hochpunkt bei
vor. Wir setzen
noch in
ein, um den y-Wert des Hochpunktes zu bestimmen:
,
d.h. .
Wendepunkte:
Notwendige Bedingung für Wendepunkte ist
,
d.h. .
EPiNweFNi: e-Funktion wird nie Null,
wird Null, für .
Einsetzen in
ergibt ,
d.h. es liegt ein Wendepunkt bei
vor. Wir setzen
noch in
ein, um den y-Wert des Wendepunktes zu bestimmen:
,
d.h. .
Weder YAS noch 0PS.
1.3 10.a)
Der Graph von
begrenzt mit den Koordinatenachsen eine Fläche
. Skizzieren Sie den Graphen
und berechnen Sie .
In dieser Aufgabenstellung ist das
Kurvendiskussionsprogramm teilweise versteckt.
Offenbar muss man die Achsenschnittpunkte
berechnen, und für die Fläche muss man aufleiten
können. Der Schnittpunkt mit der y-Achse ergibt
sich über den Funktionswert an der Stelle Null:
.
Schnittpunkte mit der x-Achse ergeben
sich über Nullstellen der Funktion :
,
,
.
Offenbar muss man für die gesuchte Fläche
die Funktion von
bis
integrieren.
Wir wissen, dass die Stammfunktion von
die Funktion
ist, was wir durch Ableiten leicht überprüfen können. Für die Fläche gilt dann:
(vgl.
Skizze).
In gleicher Weise lassen sich die Flächen der Teilaufgaben 10.b-d) berechnen: 10.b)
, 10.c)
und
10.d) .